Recursion is impractical
이 포스팅을 시작한 계기이다.
명확히 하자면, recursion은 큰 문제를 작고 동일한 문제들로 만드는데 효과적인 방법이다.
그렇기에, 코드의 가독성을 향상 시켜준다.
글을 읽기전 추천해줄 자료들
본글의 목표
: 자바스크립트 recursion에 대한 깊은 이해,
recursion이 사용되면 좋을 법한 사례들에 대한 이해,
기존의 코드를 recursion을 활용하여 새로 써보기
recursion의 좋은예시와 나쁜예시 알아보기
프로그래밍에서 recursion이란 무엇일까?
recursion이란 function 그 자체가 반복적으로 호출 될 때를 가르킨다.
모든 recursive function은 무조건 base case를 가지고 있어야 한다.( 무한하게 반복되는 recursive function을 방지! )
base case란 자신을 호출하는 것 대신에 값을 리턴해주는 function을 불러오는 특정 조건이다.
base case가 생략되거나 잘못 쓰여질경우 에러가 발생한다.
'Uncaught RangeError: Maximum call stack size exceeded'
Base Case를 쉽게 설명하자면
' The answer to a problem at the lowest possible level '
(가장 낮은 가능성의 수준의 대한 문제)
factorial function으로 예를 들자면, factorial의 가장 낮은 수준의 레벨을 보자면,
one factorial(1!)은 1이다
함수의 호출은 Call stack에 저장된다
call stack이란 stack 자료구조의 특정한 실행법이다.
LIFO(Last in, first out) 자료구조로써, function call이 call stack에 가장 위에 위치하고 가장 먼저 사라진다.
stack을 카드 덱이라고 생각하면 쉽다. 가장 위에 있는것을 뽑기가 제일 편하다.
Call Stack이란 무엇일까?
function들은 call stack에 저장되고,
Javascript에서 function 호출은 해당 함수에서 값이 리턴될 때 stack에서 사라진다.
하나 참고해야 할건, Js나 다른 언어에서 proper tail call optimization을 지원하고 있지 않고, 규모가 큰 data들을 이용할때 call stack overflowing 에러의 위험이 있다.
Recursive function 호출의 예시 ㅡ Factorial function
n보다 작거나 같은 모든 양의 정수의 곱
factorial of 5(5!)은 5*4*3*2*1 = 120이다.
첫째로, 5는 숫자 자체에서 1을 뺀 값이 곱해지고 이 과정을 1이 될때까지 반복한다.
동일한 작업을 여러단계로 나누어 실행합니다. 반복문으로 실행가능하지만, recursive하게도 정의 할 수 있습니다.
작업 자체를 동일한 더 작은 작업으로 나눌수 있기 때문이다.
function factorial(num) {
var nextNum = num - 1;
// Base case
if(num === 1) {
return num; // return 1;
}
return num * factorial(nextNum);
}
console.log(factorial(5)); // 120
factorial function 분석하기
첫째로 console.log가 먼저 스택에 들어간다.
그 다음, factorial(5)가 실행될것이고, 그 결과가 console.log함수로 전달된다.
factorial(5)를 입력하면, call stack은 아래와 같을 것이다.

리턴이 선언되있는 7번째 줄을 생략하고, factorial function은 num에 (이 경우는 5)
4가 전달 된 recursive function의 반환값을 곱한다.
function은 다음 값을 리턴한다.
return 5 * factorial(4)factorial(4)가 function이기 때문에, call stack에 집어 넣는다. 이 과정을 base case에 도달할 때까지 반복한다.
이 때, call stack은 다음과 같다.
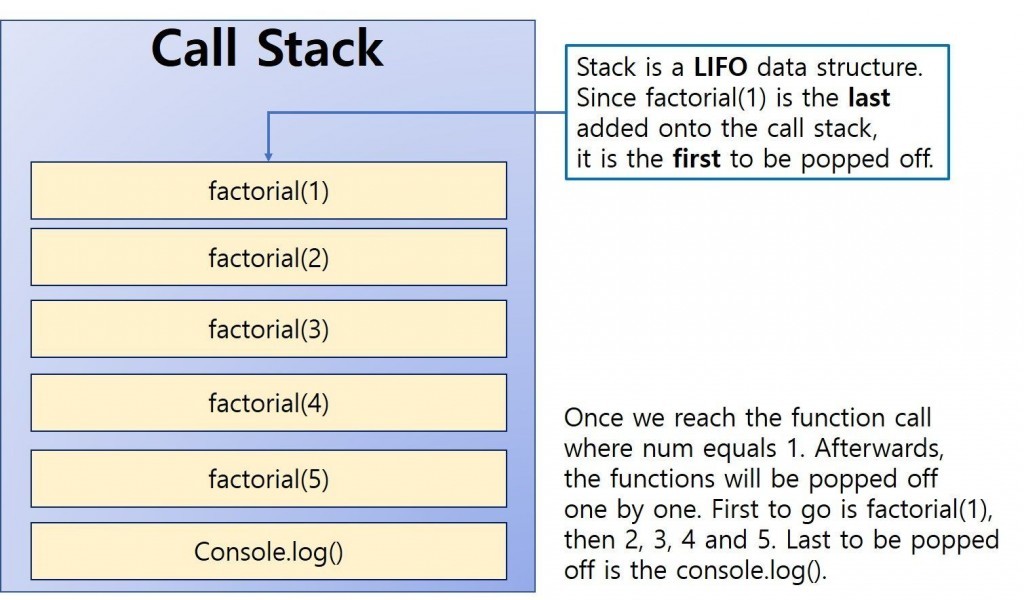
일단 base case에 도달하면, function factorial(1)은 1의 값을 리턴한다. 그러므로, 이제 factorial(1)이 1과 같다는걸 안다.
factorial(2) 또한 non-function value 2*factorial(1) 은 2*1을 리턴한다.
factorial(3)은 3 * factorial(2)은 6, fatorial(5)는 5*24 =120 까지 반복한다.

Call Stack 보는 방법
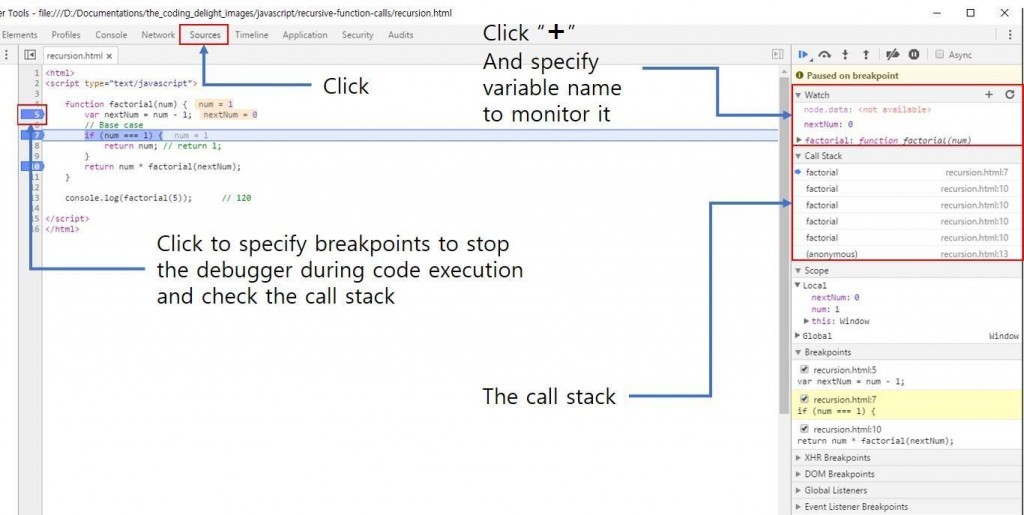
어떻게 base case를 결정할까?
user input을 고려하는게 중요하고, 때때로는 조건문을 사용하는 것이 성능을 향상 시킬 수 있다.
조건을 사용함으로써 확실한 유효성 검사를 위해 function에 맡긴다.
factorial 예시에서의 base case는 중요한 결점이 있다.
if(num === 1)처음에는 그럴듯 해보이지만, 만약 음수를 넣는다면 어떻게 될까? call tack will overflow 에러가 발생할 것이다.
또한 0을 넣는다면? 정의에 따르면 0!=1 이다. 그러므로 이 경우도 넣어주어야 한다.
if(num === 1 || num === 0)음수의 경우도 확실히 해줘야 한다. 두가지 가능한 옵션이 있다(필자의 경우 후자를 선호)
1. 0보다 큰 수 인지를 확인해주는 다른 if 문을 추가해 주는것
2. 음수의 factorial은 Math에서 undefined이기 때문에 음수는 factorial function에 전달 될 수 없다. API가 확인해 줄것이다. 각각의 recursive function call에서 음수를 불필요하게 확인하지 않게 된다.
recursion의 안좋은 사례
이전에 본 factorial 예시의 경우에도 recursive 접근이 가장 좋은 방법은 아니다.
function iterativeFactorial(num){
if(num < 0) {
throw new Error("Negative factorial results in undefined value.");
}
var result = 1;
while(num > 1) {
result *= num;
num--;
}
return result;
}위의 코드가 훨씬 간결하면서 신뢰할만하다.
궁극적으로 recursive 형식으로 나타냈을때 더 읽기 좋은가라는 질문에 관련된 것이다.
Is the code more readable when expressed in recursive format?
가독성 vs 성능
결정을 할때 성능을 고려해야 하는가?
저명한 컴퓨터 과학자 Donald Knuth는 말했다.
We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil.
Yet we should not pass up our opportunities in that critical 3%.
(시간의 97%를 차지하는 작은 효율성을 잊어버려야한다. 이른 최적화는 모든 악의 근원이다.
그러나 중요한 3%의 기회를 포기해서는 안된다.)
필자의 대답은 네 또는 아니오다.
최적화에 관련된 질문에 답을 하기전 두가지를 먼저 생각해봐라
1. 최적화가 코드의 가독성을 향상 시키는가
2. 코드를 최적화함으로써 성능에 중대한 향상이 있는가
만약 뛰어난 성능 향상이 있지만 가독성이 조금 떨어진다면 다음 개발자를 위해 서류화할만한 가치가 있다.
가독성에 관한 우선순위 규칙은 이곳에서 확인할수있다.
뛰어난 성능향상이 있을 경우에만 최적화해라.
때로는, 나쁜 코드의 경우 최적화가 가독성과 성능 둘다 향상시킬수 있다.
언제 recursion이 좋은 선택일까?
Recursion은 본질적으로 반복적인 업무이다.
그러므로, recursion은 반복적으로 실행되고 스스로 정의 될 수 있을때 최적이다.
이진탐색트리(Binary Search Tree Implementation)의 경우 생각해 볼만 하다.
binary tree 안에 각각의 하위 트리들이 그것 자체로 binary search tree이다. 이 뜻은 recursive 접근의 적절한 예시이다.
다른 예시는 merge sort 알고리즘이다. 이 알고리즘에서는 오직 한가지 엘레멘트를 가질때까지 둘로 나눈다.
결국, 반복적으로 비교하고 정렬된 컬렉션으로 병합된다. merge sort는 규모가 큰 업무를 작고 동일한 과정으로 만드는 것이다.
Recursion is a good choice when the problem at hand, or the data structure can be defined in it of itself.
(Recursion은 문제가 가까이 있거나, 자료구조 스스로 정의 될 수 있을때 좋은 선택이다.)
recursive 자료구조를 사용할 때, 아주 작은 최적화가 필요하더라도 일반적으로 가독성을 우선시 한다.
이미 복잡한 로직에 반복적으로 만들기 위해 50 줄의 코드를 추가해야한다면 좋은 경우가 아니다.
만약 간단한 for loop로 가능할 경우에는 for문을 사용하고 목적을 가지고 recursion을 사용해서는 안된다.
Recursion의 연습문제들
Warm-up
1. Reverse a string. The recursive function call should return the reversed result of the passed in string
reverseStr('cowbell') --> 'llebwoc'
2. Fibonacci number. get the nth Fibonacci number as the return value
fibonacci(5) --> 5
fibonacci(10) --> 55
fibonacci(15) --> 510
3. Count the number of reoccurring instance of a digit in a number(E.g 790923 has two 9s)
For bonus points, create a generator function using closures to create a recursive function using the value passed
>> E.g Function can generate instance such as
count7, count8which counts for the digits 7 and 8 respectively
4. Using recursion, go through a string and remove characters that occur more than once.
>> E.g passing in "Troll" should return "trol". / "abracadabra" --> "abrcd"
Intermediate
1. Find the greatest common divisor of two numbers
2. Find thr lowest common multiple of two numbers. Assums that the two numbers ar greater than or euqal to 2.
Advanced(직접 얘기해보거나, 다이어그램을 그리는것이 도움될수있다)
1. Write a binary search algorithm that accepts an array. Readers can assume that the passed in array is sorted.
2. Write your own implementation of the merge sort algorithm. As mentioned in a previous section, the merge sort algorithm divides the a big task into smaller tasks. It is one of the better scaling algorithms with a worst case performance of n log (n). The purpose of this exercise is to train the reader to be able to break down a big task into smaller tasks. Therefore, I highly recommend readers to attempt this problem without looking at the answer beforehand.
3. Try implementing a recursive data structure. A good example to start off would be implementing the binary search tree from scratch. Note: This is quite a challenging exercise, so take your time. Don’t beat yourself if you don’t get it on your first try.
'코드스테이츠(Pre)' 카테고리의 다른 글
| 자바스크립트_데이터타입과 연산자 (0) | 2019.05.28 |
|---|---|
| 자바스크립트_스코프 (0) | 2019.05.23 |
| JavaScript Reduce 자세히 알아보기 (0) | 2019.04.12 |
| array 반복을 효과적으로 하기 위한 9가지 방법 (0) | 2019.04.11 |
| filter function 이해하기 (0) | 2019.04.10 |

